Adam 和 AdamW 原理详解

本篇文章参考视频，感谢up

指数加权平均

1

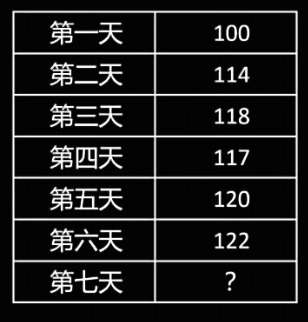
拥有前 6 天的收入，如何更准确地预测第 7 天的收入？

  1. 简单思路

取前 6 天收入的平均值，每天收入的权重为 1/6。

  1. 改进：距离现在越近的值权重越大

调整前 6 天的权重，距离今天越近的数据权重越大。

指数加权平均的思想

2

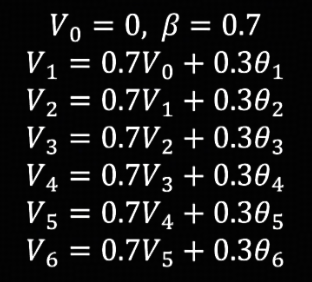
设置初始条件 $V_0 = 0$，$\beta = 0.7$，则每一天的指数加权平均值为前一天的指数加权平均值 * $\beta$ + 当天观测值 * $1 - \beta$。即 $V_t = \beta V_{t-1} + (1-\beta)\theta_{t}$

以此类推，可得到如下表达式。

3

指数加权平均用一个简单的公式实现了对历史所有值进行加权平均，而且运行过程中只需要额外保存 1 个值 $V$。

指数加权平均的问题及修正

4

初始化 $V_0=0$，取 $\beta=0.7$，计算之后发现前几天的值明显偏小。

原因是 $V_0=0$ 的初始化条件导致的，如果计算序列够长，那么计算到后面的指数加权平均时，$V_0$ 的影响就会很小，结果可以得到修正。但如果计算序列很短，该如何进行修正？

修正方法：对 $ V_0$ 初始化值进行修正。

$$V_t^{correct} = \frac{V_t}{1 - \beta^t}$$

$1 - \beta^t$ 逐渐接近于 1，当序列足够长，后面对 $V$ 的修正效果就很小了。

SGD（随机梯度下降）

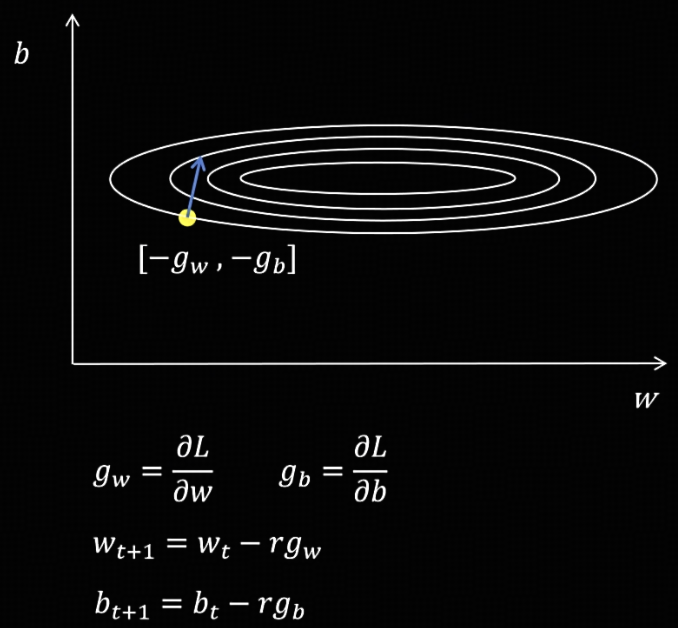
图中有两个需要优化的参数，对 w 和 b 计算损失函数的偏导得到梯度，按梯度的反方向更新参数。

问题：神经网络的参数很多，有的参数梯度很大，有的很小，更新参数时就会发生震荡，导致训练不稳定。

5

Momentum（动量梯度下降）

不用当前参数的梯度来更新参数，而是用它们从训练开始的梯度值的指数加权平均值来更新参数。

具体做法：先计算出当前时间步所有参数的梯度，然后更新所有参数当前时间步的指数加权平均值，接着再使用指数加权平均值来更新参数。

假设某个参数在各个时间步的梯度有正有负，经过指数加权平均后可以互相抵消，缓解模型训练过程中的震荡问题。

6

RMSProp

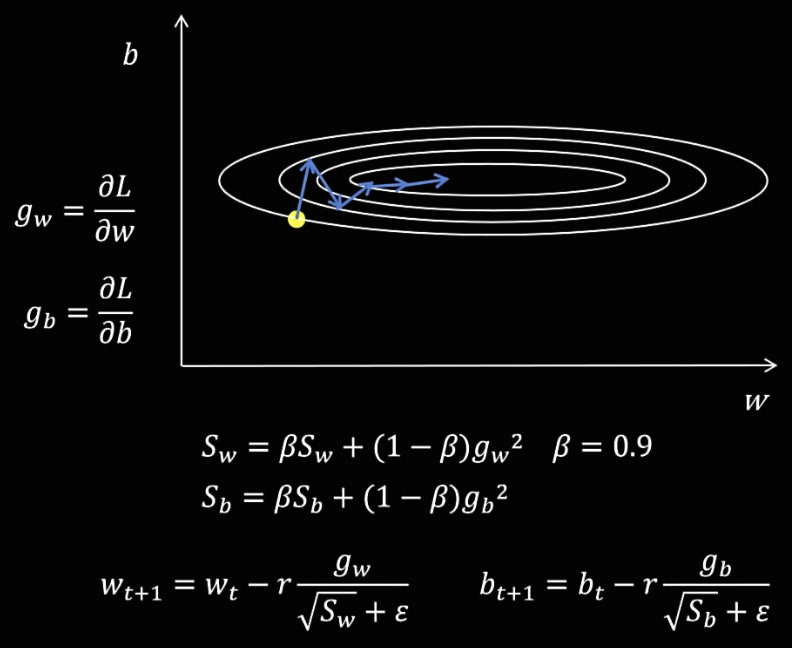
动机：训练过程中的震荡是因为有的参数的梯度很大，有的参数的梯度很小。让每个要更新的梯度都除以一个代表这个参数过去梯度大小的值，这样每个梯度就差不多大了。

具体做法：计算每个参数梯度平方的指数加权平均值 $S$，在更新参数时，用当前的梯度除以根号 $S$，避免每个参数的梯度差异过大。注意，为了防止除 0，需要在分母加上一个很小的值 $\epsilon$。

7

Adam

Adam 就是 Momentum 和 RMSProp 的结合，并修正了指数加权平均值

具体做法：首先计算参数的梯度，然后分别计算梯度（一阶矩）和梯度平方（二阶矩）的指数加权平均值并修正，最后更新参数时，使用修正后的梯度指数加权平均值和梯度平方的指数加权平均值。

8

AdamW

在 Adam 的基础上只做一点改动，那就是在更新参数时进行权重衰减，即每次更新参数后，对参数再减去一个很小的值，防止参数过大，提高模型的泛化性。AdamW 中的 W 指的就是 Weight decay。

9

Adam 与 AdamW 的区别

AdamW 不是简单的在 Adam 的基础上加 L2 正则，实现方式不一样。

Adam 加 L2 正则是在损失函数中添加正则项，而 AdamW 则是直接在更新参数时进行权重衰减，并不会修改损失函数。

  • 在 SGD 里，它们两个可以认为是等价的，得到的权重更新表达式是一样的。

10

  • 在 Adam 里，在损失函数里添加 L2 正则后会影响梯度的计算，进而影响梯度和梯度平方的指数加权平均值等后续一系列值，最后在更新参数时就不等于权重衰减了，所以 Adam 里的 L2 正则并不等于权重衰减。

11

Adam 与 AdamW 的缺点

对每个参数都要额外保存两个值：梯度的指数加权平均值和梯度平方的指数加权平均值。因为这两个值都是由梯度值进行多次累加得到的，而梯度值一般都很小，所以需要使用 float32 这种更高精度的数据格式来保存，在训练时非常占用显存。

总结

  • 指数加权平均：对越临近的值权重越大，且只用额外保存一个值。
  1. 问题：序列短时初始指数加权平均值的结果和真实值差别大；
  2. 解决：使用系数修正。

  • SGD：在梯度大的参数上容易震荡。

  • Momentum：使用历史梯度的指数加权平均值来更新参数。

  • RMSProp：训练时有的参数梯度大，有的参数梯度小，也会导致训练震荡问题，对每个参数除以每个梯度平方的指数加权平均值开根号。

  • Adam：结合了 Momentum 和 RMSProp 并对指数加权平均值进行修正。

  • AdamW：增加了权重衰减，每次更新参数后再减去一个很小的值，防止参数过大，提高泛化性。

DeepSeek 解释 AdamW 相比 Adam 所做的优化及原因

好的，我们来详细解析一下AdamW相比Adam所做的优化以及背后的原因。

简单来说，AdamW的核心优化是将“权重衰减”（Weight Decay）与“梯度下降”解耦，正确地实现了L2正则化，而不是像原始Adam那样将权重衰减与梯度计算混合在一起。

下面我们分步解释：

1. 回顾Adam和L2正则化/权重衰减

要理解AdamW，首先需要明白Adam和权重衰减是怎么工作的。

  • Adam优化器：是RMSProp和Momentum的结合体。它通过计算梯度的一阶矩（均值）和二阶矩（未中心化的方差）的指数移动平均来调整每个参数的学习率，并进行偏差校正，使得每一步更新都更加稳定和高效。
  • L2正则化：是一种防止模型过拟合的技术。它在原始的损失函数上增加一个惩罚项，这个惩罚项是所有权重参数的平方和乘以一个系数（λ 或 weight_decay）。
    • 损失函数变为：$L_{new} = L_{original} + \frac{\lambda}{2} \sum ||w||^2$
  • 权重衰减（Weight Decay）：在标准的SGD优化器中，对上述损失函数求导后，L2正则化等价于在更新权重时，每次都先让权重乘以一个略小于1的数（1 - λ），然后再减去学习率乘以梯度。 这个过程被称为“权重衰减”，因为它让权重在每次更新时都会自然地缩小一点。
    • SGD with Weight Decay的更新规则：$w_{t+1} = w_t - \eta \cdot \nabla w_t - \eta \lambda w_t$

2. 原始Adam的问题：L2正则化与权重衰减的不等价性

问题就出在这里。在原始Adam的实现中，开发者错误地将“L2正则化”和“权重衰减”视为完全等价的概念。

  1. 原始Adam的实现（Adam with L2 regularization）：

    • 在计算梯度时，损失函数已经包含了L2正则项：$\nabla L = \nabla L_{original} + \lambda w_t$
    • Adam会像处理普通梯度一样处理这个$\lambda w_t$项。它会计算这个合并后梯度（$\nabla L$）的动量和方差，并用它们来更新权重。

  2. 这为什么是个问题？

    • Adam的自适应学习率机制干扰了L2正则化的效果。Adam会为每个参数计算不同的、自适应的学习率。这意味着L2正则项（$\lambda w_t$）也被除以了梯度的平方和的平方根（即$\sqrt{v_t}$）。
    • 导致的结果是：权重衰减的效果不再是一个稳定的、与梯度无关的线性衰减，而是变成了一个与梯度历史相关的、动态的衰减。衰减的量会因参数而异，并且不稳定。
    • 换句话说，L2正则化提供的权重衰减效果，依赖于Adam为当前参数计算出的自适应学习率，这违背了权重衰减的初衷（一个稳定、一致的收缩力）。

3. AdamW的解决方案：解耦权重衰减

AdamW（Adam with Weight Decay）的提出正是为了修正上述问题。它的核心思想是：

将权重衰减作为一个独立的项，完全从梯度计算和自适应学习率的过程中分离出来。

  1. 具体做法：

    • 在计算梯度时，只使用原始的损失函数，不再包含L2正则项：$\nabla L = \nabla L_{original}$
    • 在最后更新权重的步骤中，像SGD那样，显式地、直接地减去权重衰减项。

  2. AdamW的更新公式（关键步骤）：

    • 计算梯度：$g_t = \nabla L_{original}(w_t)$ （注意：这里没有λw项了！）
    • 计算动量和方差：$m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t$， $v_t = \beta_2 v_{t-2} + (1 - \beta_2)g_t^2$
    • 偏差校正：$\hat{m_t} = \frac{m_t}{1-\beta_1^t}$， $\hat{v_t} = \frac{v_t}{1-\beta_2^t}$
    • 更新权重：$w_t = w_{t-1} - \eta \cdot (\frac{\hat{m_t}}{\sqrt{\hat{v_t}} + \epsilon} + \lambda w_{t-1})$ （注意：λw是直接加在最后的）

    可以看到，权重衰减项 λw 是独立于自适应梯度 (m_hat / sqrt(v_hat)) 之外的，它没有被除以 sqrt(v_hat)。

4. 为什么要这么做？（AdamW的优势）

  1. 正确的正则化效果：AdamW实现了真正的、纯粹的权重衰减，其衰减力度是稳定且一致的（由超参weight_decay直接控制），不再受自适应学习率的干扰。这更符合权重衰减的设计初衷。

  2. 更好的泛化性能：大量实验表明（尤其是在训练深度学习模型如ResNet、Transformer时），使用AdamW通常比使用原始Adam（Adam with L2 reg）能够获得更低的测试误差，即模型具有更好的泛化能力。这意味着模型在训练集和未见过的测试集上都表现得更好。

  3. 超参数更稳定：由于权重衰减被解耦，weight_decay超参数的行为变得更加可预测和稳定。在原始Adam中，你需要同时调整学习率（lr）和权重衰减率（λ），而这两个超参数的效果因自适应学习率而耦合在一起，调参非常困难。在AdamW中，它们的调节相对更独立。

总结对比

特性 原始Adam (with L2) AdamW (with Weight Decay)
核心思想 将L2正则项融入损失函数，作为梯度的一部分 将权重衰减作为与梯度独立的操作
梯度计算 $\nabla L = \nabla L_{original} + \lambda w$ $\nabla L = \nabla L_{original}$
权重衰减实现 通过修改后的梯度，间接被自适应学习率影响 在更新步骤中直接应用，不受自适应学习率影响
效果 权重衰减不稳定，效果不可预测 实现真正、稳定的权重衰减
性能 泛化能力通常较差 泛化能力更好，成为当前主流
调参 lr和weight_decay耦合，难调 lr和weight_decay相对独立，更易调

因此，AdamW并不是对Adam自适应学习率机制的改变，而是对其正则化方式的修正。它确保了权重衰减的正确应用，从而在实践中几乎全面优于原始的Adam实现，并成为了当今训练深度学习模型（尤其是Transformer架构）的默认优化器。现在当你看到论文或代码中使用 AdamW 时，你就知道它使用的是这种更先进的权重衰减处理方式。

DeepSeek 解释 Adam 的自适应学习率机制

好的，我们来详细解析 Adam 优化器的核心：自适应学习率机制。

Adam（Adaptive Moment Estimation）的自适应学习率机制是其强大性能的关键。它并非使用一个全局的、固定的学习率，而是为神经网络中的每一个参数计算并维护一个独立、自适应变化的学习率。

这个机制主要通过两个核心思想来实现：

  1. 动量（Momentum）：加速收敛并减少振荡。
  2. 自适应学习率（RMSProp）：根据梯度历史调整每个参数的学习率。

下面我们一步步拆解这个过程。

1. 核心组件：一阶矩和二阶矩

Adam 为每个参数 w 维护两个状态变量：

  • 一阶矩估计（First Moment Estimate, m）：这是梯度 g 的指数移动平均（Exponentially Moving Average）。它继承了 Momentum 优化器的思想，积累了梯度的方向趋势，类似于“速度”。

    • 作用：加速收敛并减少振荡。如果梯度持续指向一个方向，m 会增大，使参数在这个方向上加速移动；如果梯度方向频繁改变（振荡），m 会因正负抵消而减小，从而抑制振荡。

  • 二阶矩估计（Second Moment Estimate, v）：这是梯度 g 的平方的指数移动平均。它继承了 RMSProp 优化器的思想，衡量了梯度平方的历史平均值，反映了梯度幅度的变化情况。

    • 作用：自适应地调整每个参数的学习率。对于一个历史梯度很大的参数（通常是频繁更新的、重要的参数），v 值会很大，导致其有效学习率变小（更新步伐变小）。反之，对于历史梯度较小的参数（可能更新不频繁或不重要），v 值小，其有效学习率就相对较大（更新步伐变大）。这就像一个自动的“特征缩放”器。

2. 计算步骤详解

假设我们有一个参数 w，在时间步 t 计算得到其梯度 g_t。

第1步：计算一阶矩和二阶矩的移动平均

  • 更新一阶矩（动量）:
    m_t = β₁ * m_{t-1} + (1 - β₁) * g_t

    • β₁（通常设为 0.9）是动量的衰减率，控制历史动量 m_{t-1} 的权重。β₁ 越接近 1，历史动量的影响越大，优化方向越平滑。

  • 更新二阶矩（自适应学习率）:
    v_t = β₂ * v_{t-1} + (1 - β₂) * g_t²

    • β₂（通常设为 0.999 或 0.99）是平方梯度的衰减率。β₂ 越接近 1，对梯度平方的历史窗口看得越远。

第2步：偏差校正（Bias Correction）

这是一个非常关键但常被忽略的步骤。因为在训练初期（时间步 t 很小的时候），m_t 和 v_t 会被初始化为 0，导致它们在初期严重偏向于 0（即有偏估计），尤其是当 β₁ 和 β₂ 接近 1 时。

Adam 通过以下公式进行偏差校正，使得估计值变得无偏，更加准确：

  • 校正一阶矩:
    m̂_t = m_t / (1 - β₁^t)

    • t 是当前时间步。随着 t 增大，(1 - β₁^t) 会趋近于 1，校正的作用逐渐减弱。

  • 校正二阶矩:
    v̂_t = v_t / (1 - β₂^t)

第3步：参数更新

最后，使用校正后的矩估计来更新参数：

w_t = w_{t-1} - η * (m̂_t / (√(v̂_t) + ε))

  • η：全局学习率，由用户设定，是所有参数更新的基础步长。
  • m̂_t：包含了动量信息的校正后梯度方向。
  • √(v̂_t)：校正后的梯度平方的均方根（Root Mean Square）。它衡量了梯度幅度的历史规模。
  • ε：一个极小值（如 1e-8），为了防止分母为零，并保证数值稳定性。

自适应学习率机制的核心体现

现在，我们聚焦到最关键的部分：(m̂_t / (√(v̂_t) + ε))。

  • 分子 m̂_t：代表了当前参数的更新方向，它融合了当前的梯度方向和历史的动量方向，使得更新更加平滑和高效。

  • 分母 √(v̂_t)：这就是自适应学习率的来源！

    • 如果一个参数的历史梯度幅度一直很大（即 v̂_t 很大），那么 √(v̂_t) 就会很大，导致整个分式 (m̂_t / √(v̂_t)) 的值变小。这意味着该参数的有效学习率（η / √(v̂_t)）降低了，它的更新步伐会变小。这很合理，因为一个历史梯度大的参数可能已经处于一个陡峭的区域，需要小步谨慎移动。
    • 反之，如果一个参数的历史梯度幅度一直很小（即 v̂_t 很小），那么 √(v̂_t) 就小，分式 (m̂_t / √(v̂_t)) 的值就相对较大。这意味着该参数的有效学习率变大了，它的更新步伐会变大。这也合理，因为一个历史梯度小的参数可能处于一个平坦的盆地，可以更大胆地前进。

直观比喻

可以把参数更新想象成开车下山：

  • 动量 (m_t)：就像车的速度和惯性。如果一直朝一个方向开，车速会越来越快（加速收敛）；如果频繁转弯，车速会慢下来（减少振荡）。
  • 自适应学习率 (v_t)：就像根据路况调整油门。如果路很陡（梯度大），就轻踩油门（小学习率），小心慢行。如果路很平缓（梯度小），就重踩油门（大学习率），快速通过。
  • Adam：同时具备了强大的惯性（动量）和智能的油门控制系统（自适应学习率）。它知道什么时候该加速，什么时候该减速，并且为每个轮子（每个参数）都配备了独立的油门控制系统。

总结：Adam自适应学习率的优势

  1. 参数独立性：为每个参数计算独立的自适应学习率，非常适合处理稀疏梯度或不同特征尺度差异很大的数据。
  2. 兼顾动量和自适应：同时吸收了 Momentum 和 RMSProp 的优点，既能加速收敛、减少振荡，又能根据梯度幅度智能调整步长。
  3. 偏差校正：解决了训练初期估计偏差的问题，使得初期更新更加准确。
  4. 实践效果好：由于其鲁棒性和高效性，Adam 及其变体（如AdamW）成为训练深度神经网络最流行和最常用的优化器之一。

正是因为这种精细且自适应的机制，Adam 能够非常高效地 navigating 复杂的损失函数景观，找到最优或接近最优的解。

Machine Learning > Deep Learning
#Adam #AdamW
Adam 和 AdamW 原理详解
https://cosmoliu2002.github.io/posts/adam-adamw-detail/
作者
LiuYu
发布于
2025年9月4日
许可协议