灵神基础算法精讲-11-学习笔记

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

思路1

在递归的时候，除了传入节点，还需要传入这个开区间的范围，对于每个节点，先判断它的节点值是否在开区间内，然后再往下递归，那如果往左边递归，那就把开区间的右边界更新为节点值，如果往右递归，那就把开区间的左边界更新为节点值，这种先访问节点值，再递归左右子树的做法叫做前序遍历，特别注意根节点，也就是函数调用的入口，再往上它是没有节点的，在这种情况下，需要传入负无穷和正无穷。

首先增加函数的传入参数-开区间的左右边界，设置它们的默认值分别为 -inf 和 inf，首先判断递归的边界条件，也就是判断节点是否为空，若为空，返回 True，然后记录一下节点值为 x，首先它必须在开区间内，所以它是 left < x < right，同时左子树必须是二叉搜索树，那么区间的右边界更新为 x，同时右子树也必须是二叉搜索树，那么区间的左边界更新为 x，

做法1

def isValidBST(root, left = -inf, right = inf):
    if root is None:
        return True
    x = root.val
    return left < x < right and isValidBST(root.left, left, x) and isValidBST(root.right, x, right)

思路2

按照递归左子树访问节点值，再递归右子树这样的顺序去遍历，这样就可以得到一个严格递增数组，只需要比较所有相邻的元素就可以判断一个数组是严格递增的，对于二叉搜索树来说，按照左子树->节点值->右子树这样的顺序遍历，遍历完左子树，就可以看当前的节点值是否大于上一个节点的值，然后把当前节点值记录下来，那它的下一个节点值就和它比大小，这就是中序遍历。

由于第一个节点没有上一个节点，所以可以初始化它的上一个节点的值为 -inf，然后就可以开始递归了，首先判断边界条件，如果节点为空，还是返回 True，然后递归左子树，如果左边不行，直接返回 False，然后比较一下，如果节点值小于等于上一个节点，就返回 False，然后将节点值赋值给 pre，最后返回递归右子树。

做法2

pre = -inf
def isValidBST(root):
    
    if root is None:
        return True
    if not isValidBST(root.left):
        return False
    if root.val <= pre:
        return False
    pre = root.val
    return isValidBST(root.right)

思路3

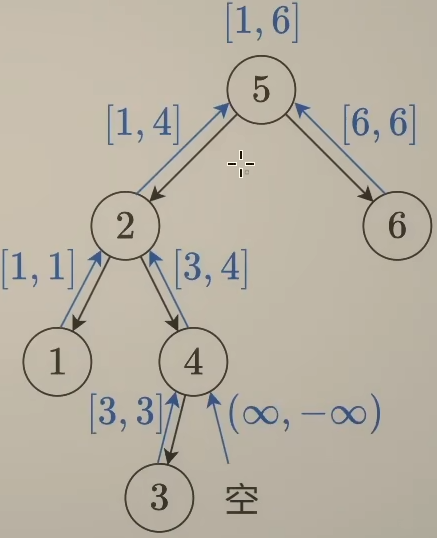
之前的前序遍历是把节点值的范围往下传，那么还可以把节点值的范围往上传，比如对于 5 来说，它的左子树节点值的范围是 [1, 4]，右子树范围是[6, 6]，那么 5 大于左边的最大值，并且 5 小于右边的最小值，这是合法的，这种做法需要先遍历左右子树，再判断节点值，这就是后序遍历。节点值范围的最小值和最大值都需要返回，为了简化代码逻辑，如果递归到空节点，对于这种情况，可以返回正无穷到负无穷。如果中途发现它不是一颗二叉搜索树，可以额外返回一个 False，或者返回负无穷到正无穷，这样可以保证返回之后，上面的节点通过比较大小，也会认为它不是一颗二叉搜索树。

首先写一个递归函数，递归函数传入参数为一个节点，首先判断边界条件，如果当前节点为空，返回正无穷到负无穷。然后递归左子树，拿到左边的最小值和最大值，然后递归右子树，拿到右边的最小值和最大值，记一下节点值，如果节点值小于等于左边的最大值，或者大于等于右边的最小值，那么它就不是一颗二叉搜索树，返回负无穷到正无穷，从这里可以发现，上面返回正无穷和负无穷可以使得这个条件判断一定不成立。最后返回左边的最小值和右边的最大值。由于这里会返回正无穷和负无穷，所以对于左范围，要取当前节点值和左边最小值中的更小者，取当前节点值和右边最大值中的更大者。最后递归完了之后，看一下拿到的右边范围是不是无穷大，如果是，就表示它不是一颗二叉搜索树。

做法3

def isValidBST(root):
    def f(node):
        if node is None:
            return inf, -inf
        l_min, l_max = f(node.left)
        r_min, r_max = f(node.right)
        x = node.val
        if x <= l_max or x >= r_min:
            return -inf, inf
        return min(l_min, x), max(r_max, x)
    return f(root)[1] != inf