灵神基础算法精讲-15-学习笔记

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

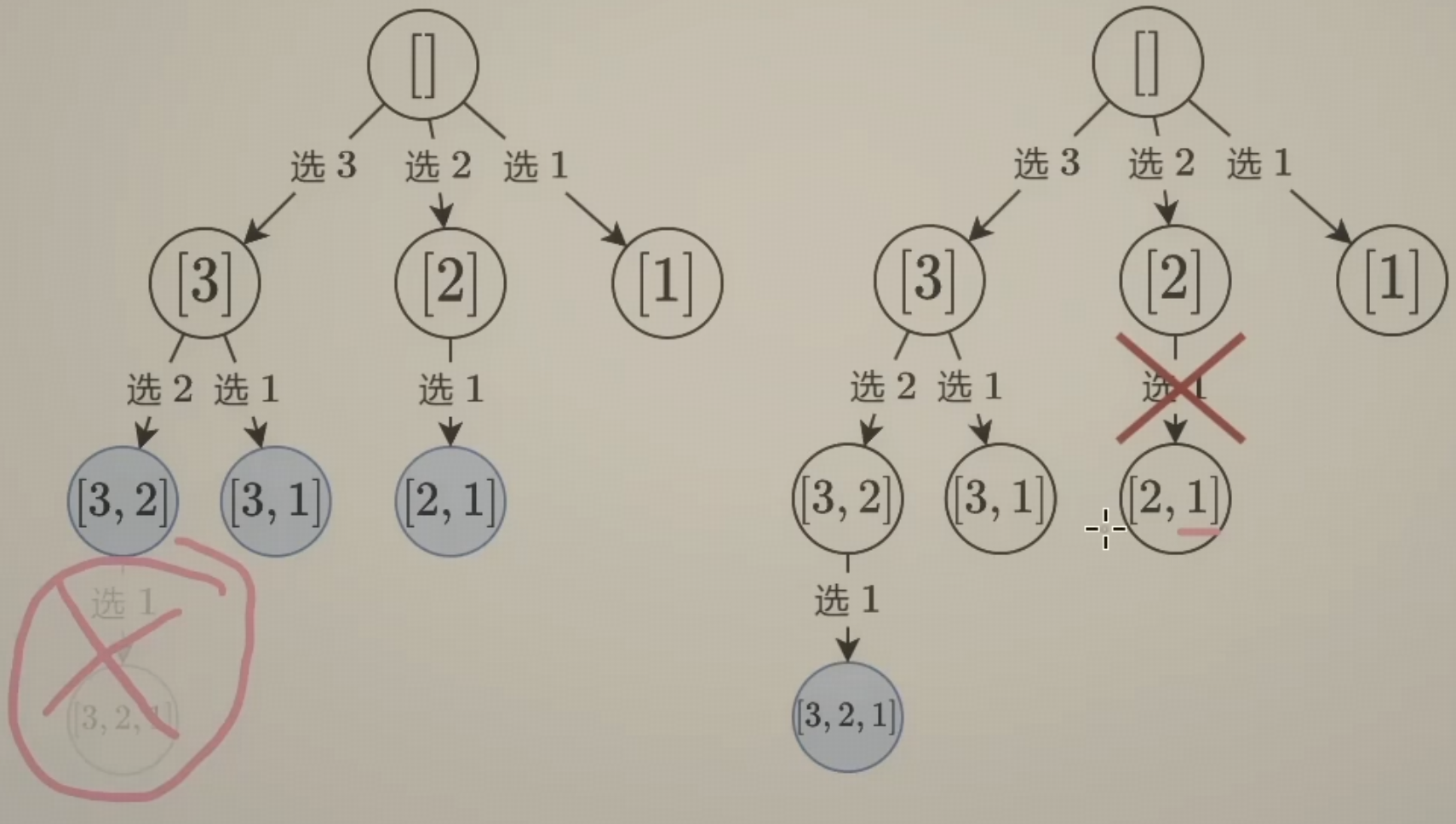
思路

回顾子集型回溯，如果要从 3， 2， 1 中选出子集，按照每次选一个数的做法，可以得到一颗搜索树，搜索树每一层的数字个数是相同的，他们恰好可以表示从三个数中选择一个数的三种情况，选择两个数的三种情况和选择三个数的一种情况，这刚好就是我们要求的组合问题。

所以只需要在求子集的基础上，增加一个判断逻辑。比如需要选两个数，那就在路径长度等于 2 时记录答案，然后 return。再比如选三个数的情况，如果第一个数选的是 2，就不需要再递归了，因为继续递归后面只能选 1 了，无法选三个数，所以一定无法找到答案，因此可以提前 return，不再递归。

相比子集问题，组合问题是可以做一些额外优化的。

假设 path 长为 m，那么还需要选 d = k - m 个数，从大到小枚举，设当前需要从 [1, i] 这 i 个数中选数，如果 i < d，最后必然无法选出 k 个数，不需要继续递归。这是一种剪枝技巧。

1

做法

  1. 枚举下一个数选哪个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        ans = []
        path = []

        def dfs(i: int) -> None:
            d = k - len(path)  # 还要选 d 个数
            if d == 0:  # 选好了
                ans.append(path.copy())
                return
            # 枚举的数不能太小，否则后面没有数可以选
            for j in range(i, d - 1, -1):
                path.append(j)
                dfs(j - 1)
                path.pop()  # 恢复现场

        dfs(n)  # 从 i=n 开始倒着枚举
        return ans
  1. 选或不选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        ans = []
        path = []

        def dfs(i: int) -> None:
            d = k - len(path)  # 还要选 d 个数
            if d == 0:  # 选好了
                ans.append(path.copy())
                return

            # 不选 i
            if i > d:
                dfs(i - 1)

            # 选 i
            path.append(i)
            dfs(i - 1)
            path.pop()  # 恢复现场

        dfs(n)  # 从 i=n 开始倒着枚举
        return ans

时间复杂度：叶子的个数乘上从根到叶子的路径长度，O(k * C(n, k))。
空间复杂度：O(k)。

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字1到9
  • 每个数字 最多使用一次
    返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

思路

在上一题的基础上增加一个条件：选出的 k 个数加起来恰好等于 n。

最简单的思路是在上一题的基础上加个判断，在记录答案之前判断一下，当路径元素和恰好等于 n 时才记录答案。

剪枝：

  1. 剩余数字个数不够 i < d。
  2. 假如选的元素之和已经超过 n 了，那么就不需要继续递归了。倒过来思考，看成是需要选和为 t 的数值，t 表示 target。一开始调用时传入 n，每选一个数字 j 就把这个 target 减小 j，如果 target < 0，直接 return。
  3. 剩余数字即使全部选最大的，和也不够 t，例如 i = 5，还需要选 d = 3 个数，那么如果 t > 5 + 4 + 3，可以直接返回。用等差数列之和来简化计算。

做法

  1. 枚举选哪个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        ans = []
        path = []

        def dfs(i: int, left_sum: int) -> None:
            d = k - len(path)  # 还要选 d 个数
            if left_sum < 0 or left_sum > (i * 2 - d + 1) * d // 2:  # 剪枝
                return
            if d == 0:  # 找到一个合法组合
                ans.append(path.copy())
                return
            # 枚举的数不能太小，否则后面没有数可以选
            for j in range(i, d - 1, -1):
                path.append(j)
                dfs(j - 1, left_sum - j)
                path.pop()  # 恢复现场

        dfs(9, n)  # 从 i=9 开始倒着枚举
        return ans
  1. 选或不选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        ans = []
        path = []

        def dfs(i: int, left_sum: int) -> None:
            d = k - len(path)  # 还要选 d 个数
            if left_sum < 0 or left_sum > (i * 2 - d + 1) * d // 2:  # 剪枝
                return
            if d == 0:  # 找到一个合法组合
                ans.append(path.copy())
                return

            # 不选 i
            if i > d:
                dfs(i - 1, left_sum)

            # 选 i
            path.append(i)
            dfs(i - 1, left_sum - i)
            path.pop()

        dfs(9, n)
        return ans

时间复杂度：O(k * C(9, k))。
空间复杂度：O(k)。

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

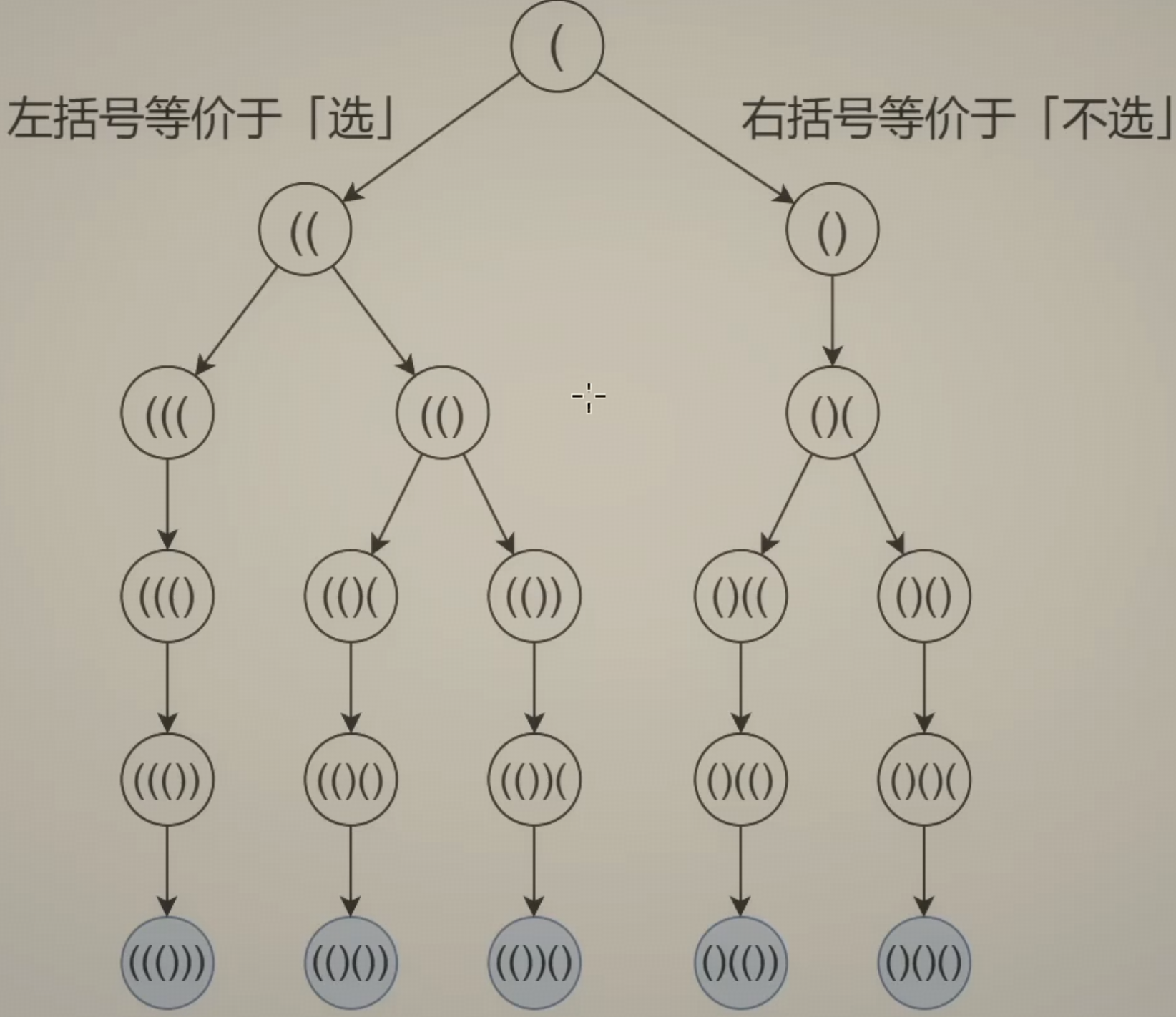
思路

从 2n 个位置中选 n 个位置放左括号，对于第 i 个位置，如果选它就填左括号，否则填右括号。既然选和不选都需要填一个字符，那么就用选和不选的思路来做，用这个思路可以得到一颗搜索树，比如 n = 3 时，那么左括号的个数不能超过 3，一旦已经选了 3 个左括号，就只能填右括号了，同时，右括号的个数也不能超过左括号的个数，比如，左右括号相等的时候，就只能选左括号了。

2

3

还需要记录左括号的个数 open，只要 open < n 就可以选左括号。

右括号的个数为 i - open，如果右括号的个数小于左括号的个数，即 i - open < open，就可以选右括号。

做法

  1. 枚举当前位置填左括号还是右括号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        ans = []
        path = [''] * (n * 2)  # 所有括号长度都是 2n

        # 目前填了 left 个左括号，right 个右括号
        def dfs(left: int, right: int) -> None:
            if right == n:  # 填完 2n 个括号
                ans.append(''.join(path))
                return
            if left < n:  # 可以填左括号
                path[left + right] = '('  # 直接覆盖
                dfs(left + 1, right)
            if right < left:  # 可以填右括号
                path[left + right] = ')'  # 直接覆盖
                dfs(left, right + 1)

        dfs(0, 0)  # 一开始没有填括号
        return ans
  1. 枚举下一个左括号的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        ans = []
        path = []  # 记录左括号的下标

        # 目前填了 i 个括号
        # balance = 这 i 个括号中的左括号个数 - 右括号个数
        def dfs(i: int, balance: int) -> None:
            if len(path) == n:
                s = [')'] * (n * 2)
                for j in path:
                    s[j] = '('
                ans.append(''.join(s))
                return
            # 枚举填 right=0,1,2,...,balance 个右括号
            for right in range(balance + 1):
                # 先填 right 个右括号，然后填 1 个左括号，记录左括号的下标 i+right
                path.append(i + right)
                dfs(i + right + 1, balance - right + 1)
                path.pop()  # 恢复现场

        dfs(0, 0)
        return ans

时间复杂度：O(n * C(2n, n))。
空间复杂度：O(n)。

LeetCode
#回溯
灵神基础算法精讲-15-学习笔记
https://cosmoliu2002.github.io/posts/combinatorial-backtracking/
作者
LiuYu
发布于
2024年12月31日
许可协议