机器学习之树模型
决策树
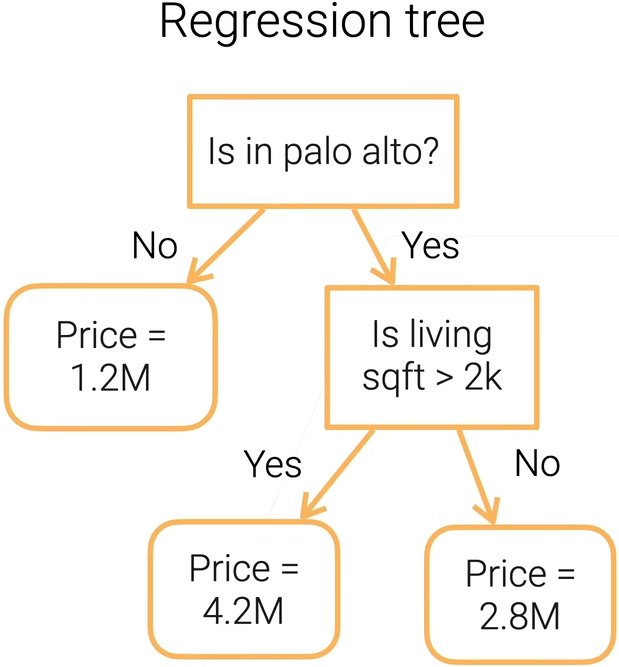
决策树顾名思义就是用决策树来做决定,可分为分类树和回归树,如下所示。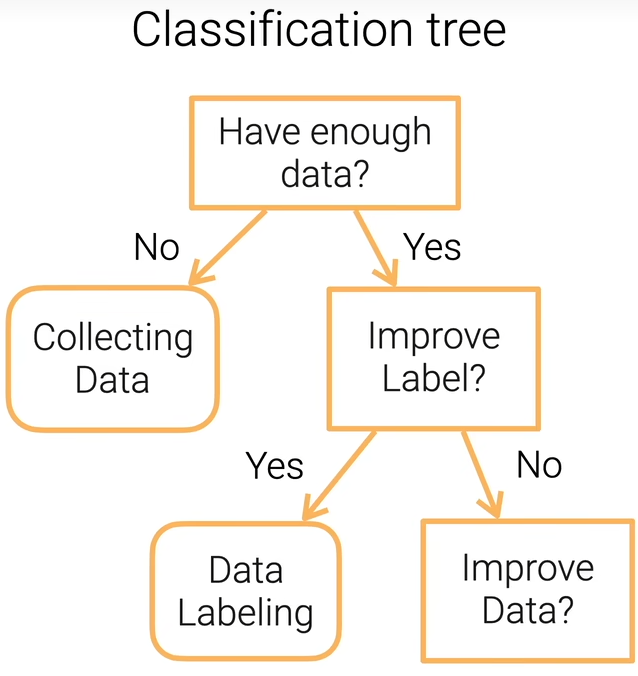
优点:
- 模型可解释。
- 可处理数值和类别的特征。
缺点:
- 非常不稳定(集成学习可解决这个问题)。
- 复杂的决策树会造成过拟合(剪枝可解决这个问题)。
- 难以并行计算。
随机森林(Bagging)
随机森林的想法是既然一棵树不行,那就生成很多棵树。训练多个决策树来提升稳定性。每棵树独立地进行训练,训练结束后,所有树一起作用来产生结果(若是分类任务,则进行投票,比如超过一半的树觉得它是1的话,那么它就是1)。
随机森林的代价: 昂贵的训练和预测成本。
如果不是随机产生的树,那么对稳定性的提升是有限的,所以随机是必须的。
随机来自于两种情况。
第一种随机性叫做Bagging,训练一棵树的时候用了一个训练集,然后在这个训练集里面随机采样一些样本,每次随机采样一个样本,记下这个样本,再把这个样本放回去,循环往复,假设样本是[1, 2, 3, 4, 5],做Bagging的时候随机采样5个样本[1, 2, 2, 3, 4],可以看到,Bagging采样得到的样本可能是重复的。拿到一个Bagging出来的数据集之后,就在上面训练一棵树,然后一直重复,直到训练n棵树为止。
第二种随机性是把Bagging出的数据拿出来之后,再随机采样一些特征列出来,不要使用整个特征,如果树是一个表的话,先随机采样一些行,再随机采样一些列,这里不会采样到两个完全一样的行或列。
所以对于每一棵树的训练,不管是对于样本还是特征来说,都跟其它树是不一样的, 这样就会产生大量随机的树,组合起来就叫做随机森林。
Gradient Boosting(基于梯度的Boosting)
按顺序训练很多棵树,这些树合在一起能得到一个比较大的模型。假如训练n棵树,从时间步t=1开始,在时刻t,用Ft(x)表示过去所有训练的树的和,就是前面训练出来的t-1棵树全部加起来,每个树是一个函数,那么Ft(x)的输出就是每个树的输出的和。接下来在时间t里训练一颗新的树ft,训练数据使用残差数据,特征x不变,标号变为样本的真实标号y-Ft(x)预测得到的标号,最后训练得到的树要跟之前所有的树加在一起。
残差等价于每一次训练一个新的树去拟合损失函数对Ft(x)函数的梯度的负数,所以叫做Gradient Boosting。
总结
- 决策树是机器学习中为数不多的可解释模型,可用作分类和回归。
- 树模型的一大问题是不稳定,它对数据的噪音非常敏感,所以可以通过将很多树放在一起来降低偏移和方差。两种常见的解决方法: Random Forest 和 Gradient Boosting Trees。
- 树模型广泛应用于工业界,训练简单,容易得到满意的结果。