灵神基础算法精讲-27-学习笔记

239.滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

思路

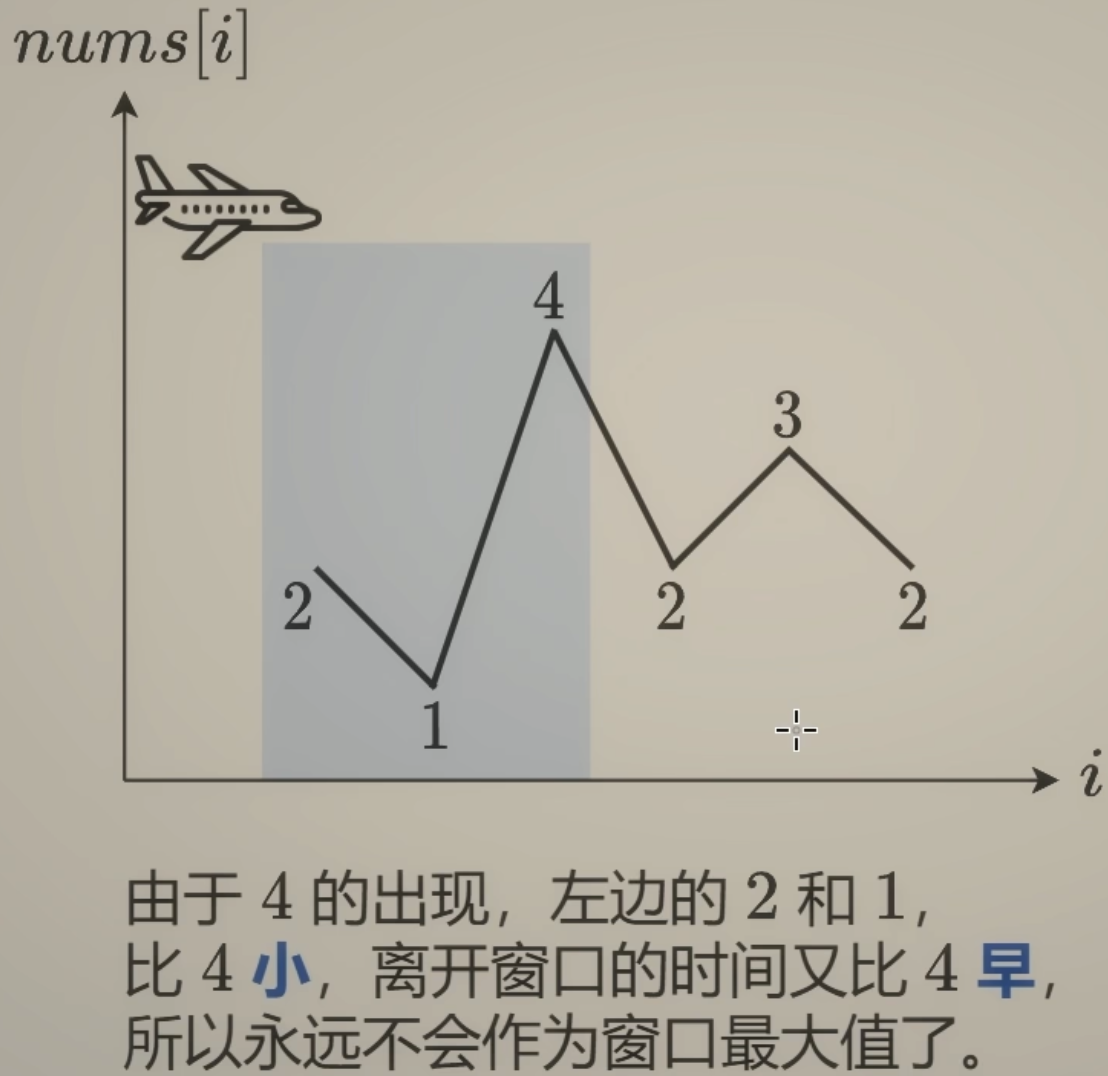
举个例子，比如数组元素为 2 1 4 2 3 2，求出每个长为 3 的连续子数组的最大值。假设我们坐在一架飞机上向下看，数组元素值为山的高度，一开始看到 2 1 4，最高为4，随着飞机向右飞，首先遇到 2，它是有可能成为后续的最大值的，如果右边的数都比 2 小的话，但现在还不知道右边有哪些数，所以就把 2 记录下来；然后遍历到 3，由于 2 比 3 小，2 永远不可能成为最大值了，那么去掉 2，记录 3；最后遍历到 2，现在只能看到 2 3 2 了，在记录 2 之前，由于 4 已经不在视野中了，可以先把 4 去掉，再记录 2。

从上述过程中可以发现，每次遇到一个数，都把前面比它小的数去掉了，如果有相同数字也可以去掉，保留最右边那个就可以，所以记录的这些数从左到右是严格递减的，那么最大值就自然是第一个数了。

在这个过程中，有添加、删除操作，并且都是发生在最左边和最右边的，所以可以使用双端队列来实现。此外，由于元素值从队首到队尾是单调递减的，这样的双端队列也叫做单调队列。

做法

遍历数组，滑动窗口框架分为三步，第一是入，元素进入窗口，当队列不为空且队列的最后一个元素 <= nums[i]，就把队尾弹出，然后把下标 i 插入队尾；第二是出，元素离开窗口，如果 i - q[0] + 1 > k，即窗口长度大于 k，就把队首弹出；第三是记录答案，当下标 i >= k - 1 时，证明窗口长度等于 k，此时才记录答案，将队首记录到答案里。

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        ans = [0] * (len(nums) - k + 1)  # 窗口个数
        q = deque()  # 双端队列

        for i, x in enumerate(nums):
            # 1. 右边入
            while q and nums[q[-1]] <= x:
                q.pop()  # 维护 q 的单调性
            q.append(i)  # 注意保存的是下标，这样下面可以判断队首是否离开窗口

            # 2. 左边出
            left = i - k + 1  # 窗口左端点
            if q[0] < left:  # 队首离开窗口
                q.popleft()

            # 3. 在窗口左端点处记录答案
            if left >= 0:
                # 由于队首到队尾单调递减，所以窗口最大值就在队首
                ans[left] = nums[q[0]]

        return ans

复杂度分析

• 时间复杂度：O(n)，其中 n 为 nums 的长度。由于每个下标至多入队出队各一次，所以二重循环的循环次数是 O(n) 的。
• 空间复杂度：O(min(k,U))，其中 U 是 nums 中的不同元素个数（本题至多为 20001）。双端队列至多有 k 个元素，同时又没有重复元素，所以也至多有 U 个元素，所以空间复杂度为 O(min(k,U))。返回值的空间不计入。

总结

及时去掉无用数据，保证双端队列有序。

当前数字 >= 队尾，弹出队尾，弹出队首不在窗口内的元素。