旋转位置编码（RoPE）原理详解

RoPE作者苏剑林提出RoPE时的想法以及求解过程：https://spaces.ac.cn/archives/8265

本篇文章参考视频，感谢up

旋转矩阵

一个例子

旋转位置编码的核心是通过由 sin 和 cos 函数构成的二维旋转矩阵对二维向量进行旋转，$\theta$ 是旋转角度。比如针对 x 轴上的 (1, 0) 向量，旋转 $\theta$ 角，其长度不会改变，旋转后的向量等于原向量 * $\theta$ 角旋转矩阵。

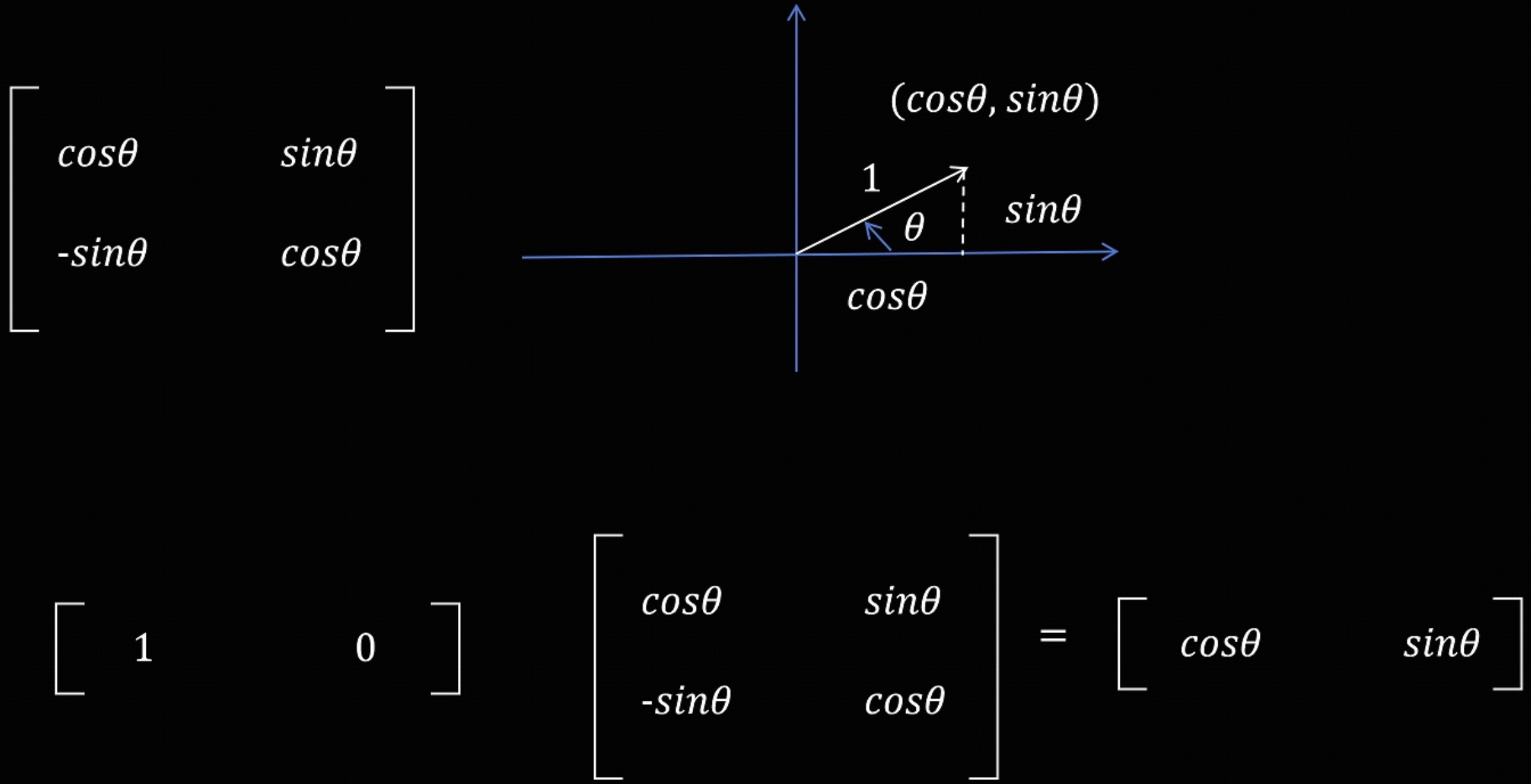
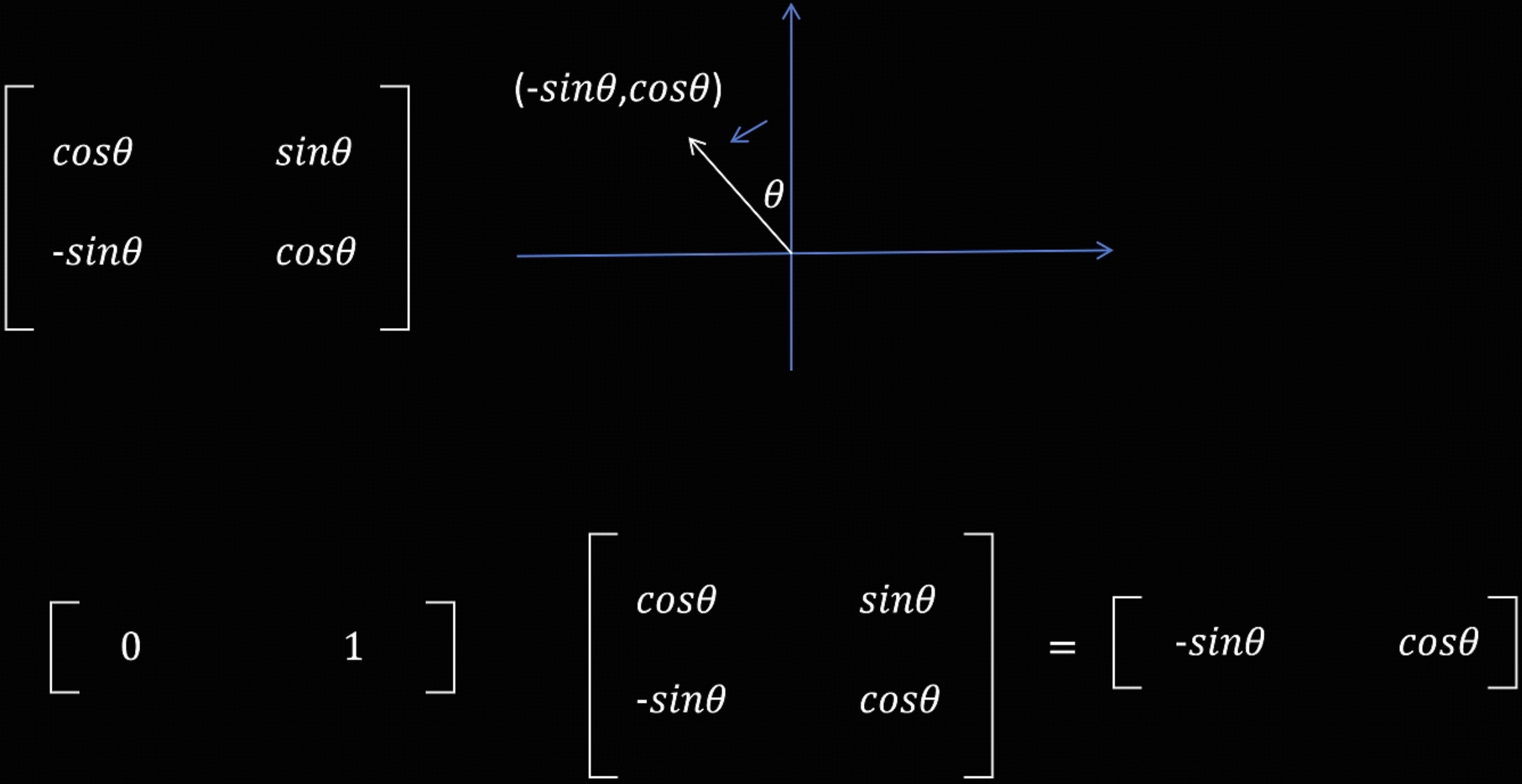
(1, 0) 和 (0, 1) 是坐标系的一个基，这个基通过旋转矩阵都逆时针旋转了 $\theta$ 角，那么这个基里所有的向量都跟着被旋转了 $\theta$ 角。

旋转矩阵的作用

假设一个向量长度为 r，其与 x 轴的夹角为 $\theta$，旋转矩阵为逆时针旋转 $\beta$，通过矩阵乘法可得到如下表示，最后利用三角公式可以得到：经过旋转的向量与原始向量相比，其长度不变，角度逆时针旋转了 $\theta$ 角。

旋转矩阵的两个性质

1. 一个向量先旋转 $\theta_1$，再旋转 $\theta_2$，等于一次性旋转 $\theta_1+\theta_1$。

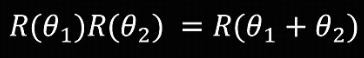
1. 角度为 $\theta$ 的旋转矩阵的转置等于角度为 $-\theta$ 的旋转矩阵。

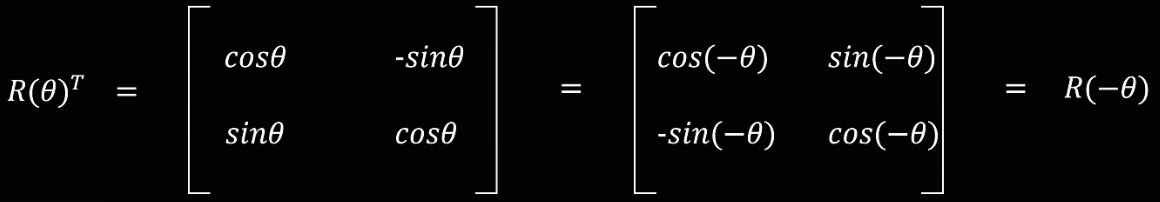
相对位置编码

二维向量示例

注意力机制中需要计算 q 和 k 的点积，等价于 q * k 的转置，直接计算点积是没有考虑位置信息的。如果 q 的位置是 m， k 的位置是 n，那么对 q 旋转 m，对 k 旋转 n，再做点积，得到的结果就包含了它们之间的相对位置信息。

扩展到高维向量

将维度两两组合在一起进行旋转，两个特征维度为一组，每组在它们两个特征组成的子空间内进行旋转。特征的组合可以随意选取，任意两个特征为一组都可以。

图中的 m 代表位置，比如处于序列第一个位置的 token 的 m 就为0，以此类推；f 代表 sin 和 cos 的频率，在这个公式里，频率最大的是第一个二维子空间，频率为 1，频率最小的是最后一个二维子空间，频率接近 10000。

不同频率的三角函数对应不同尺度的位置信息。低频信号变化缓慢，适合编码长距离依赖（远距离token之间的关系）；高频信号变化迅速，适合编码短距离依赖（邻近token之间的关系）。若所有子空间频率相同，模型只能捕捉到单一尺度的位置模式（如仅能区分相邻词，无法建模长句依赖）。

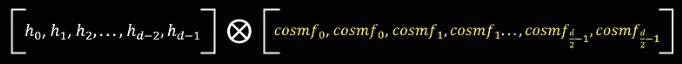
通过上述计算方式来实现 RoPE，使用图中向量逐位对应相乘。

HuggingFace 中 Llama 的 RoPE 代码实现

1. 计算频率

# torch.arange(0, self.dim, 2) → 形状为 [self.dim // 2] 的向量，生成从 0 到 dim-2 的偶数索引序列（步长为 2）
# 计算每个维度位置对应的频率值，最终 inv_freq 形状：[self.dim // 2]
inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2, dtype=torch.int64).float().to(device) / self.dim))

其中，self.base 为 10000。

2. 计算正弦值和余弦值

def forward(self, x, position_ids, seq_len=None):
    # 输入 position_ids 形状：[batch_size, seq_len]
    # self.inv_freq[None, :, None] → [1, dim//2, 1]
    # .expand(position_ids.shape[0], -1, 1) → [batch_size, dim//2, 1]
    inv_freq_expanded = self.inv_freq[None, :, None].float().expand(position_ids.shape[0], -1, 1)

    # position_ids[:, None, :] → [batch_size, 1, seq_len]
    position_ids_expanded = position_ids[:, None, :].float()
    
    # [batch_size, dim//2, 1] @ [batch_size, 1, seq_len] → [batch_size, dim//2, seq_len]
    # .transpose(1, 2) → [batch_size, seq_len, dim//2]
    freqs = (inv_freq_expanded.float() @ position_ids_expanded.float()).transpose(1, 2)

    # 沿最后一个维度拼接两个相同张量，输出形状：[batch_size, seq_len, dim]
    emb = torch.cat((freqs, freqs), dim=-1)

    # 对 emb 逐元素计算余弦/正弦，保持形状
    cos = emb.cos()
    sin = emb.sin()
    
    return cos.to(dtype=x.dtype), sin.to(dtype=x.dtype)

3. 对 q 和 k 添加旋转位置编码信息

def rotate_half(x):
    # 将最后一个维度分成两半：x1 和 x2，输出形状不变
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)

def apply_rotary_pos_emb(q, k, cos, sin, position_ids=None, unsqueeze_dim=1):
    """Applies Rotary Position Embedding to the query and key tensors...."""
    # cos/sin.unsqueeze(unsqueeze_dim) → [batch_size, 1, seq_len, dim] (默认 unsqueeze_dim=1)
    cos = cos.unsqueeze(unsqueeze_dim)
    sin = sin.unsqueeze(unsqueeze_dim)

    # q/k 输入形状: [batch_size, num_heads, seq_len, head_dim](head_dim = dim)
    # q * cos：广播后 [batch_size, num_heads, seq_len, dim]，rotate_half(q) * sin：相同形状
    q_embed = (q * cos) + (rotate_half(q) * sin)
    k_embed = (k * cos) + (rotate_half(k) * sin)

    # 输出 q_embed/k_embed 形状与输入 q/k 相同
    return q_embed, k_embed

对于与 sin 相乘的 q 和 k 需要有一半是负值，但是不一定要按照原始公式来实现，只需要保证其中有一半是负值即可，负值元素可以任意选取。

在HuggingFace论坛的讨论中，有人指出了这个问题：对于查询向量 【1, 2, 3, 4, 5, 6】，期望的输出应该是 【-2, 1, -4, 3, -6, 5】（相邻对旋转），但rotate_half函数返回的是 【-4, -5, -6, 1, 2, 3】（前后半分割）。这两种方法在数学上被认为是等价的，HuggingFace可以直接加载Meta官方发布的检查点权重，这表明两种实现在某种程度上是兼容的，另外，模型在训练过程中会学习适应特定的RoPE实现方式