灵神基础算法精讲-14-学习笔记

回溯问题套路

• 子集型回溯
  0-1背包问题也可以算作一种子集型回溯。

子集本质上就是看集合的每个元素是选它还是不选它。

比如集合有两个元素，第一个元素选或者不选，有两种情况，第二个元素同理，那么总共有2*2=4种情况。

要想生成所有子集，有两种思路，区别在于当前操作是什么。如果站在输入的角度思考，那就是枚举第i个数，选它还是不选它；子问题就是从下标大于等于i的数字中构造子集；下一个子问题就是从下标大于等于i+1的数字中构造子集。

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

思路

首先思考一个问题，如果要生成所有长为的 2 字符串，其中第一个字母在 abc 中选一个，第二个字母在 def 中选一个，那么两两组合，总共有 3x3=9 个不同的字符串。

暴力做法：写一个二重循环，外层枚举第一个字母，内层枚举第二个字母。但是，如果需要生成长为 n 的字符串，应该怎么办。从这里可以发现，单纯的循环嵌套的表达能力是有局限的。

借用递归的思路，思考原问题和子问题。原问题：构造长为 n 的字符串——枚举一个字母——子问题：构造长为 n - 1 的字符串。这种从原问题到子问题的过程适合使用递归解决，通过递归就可以达到多重循环的效果。

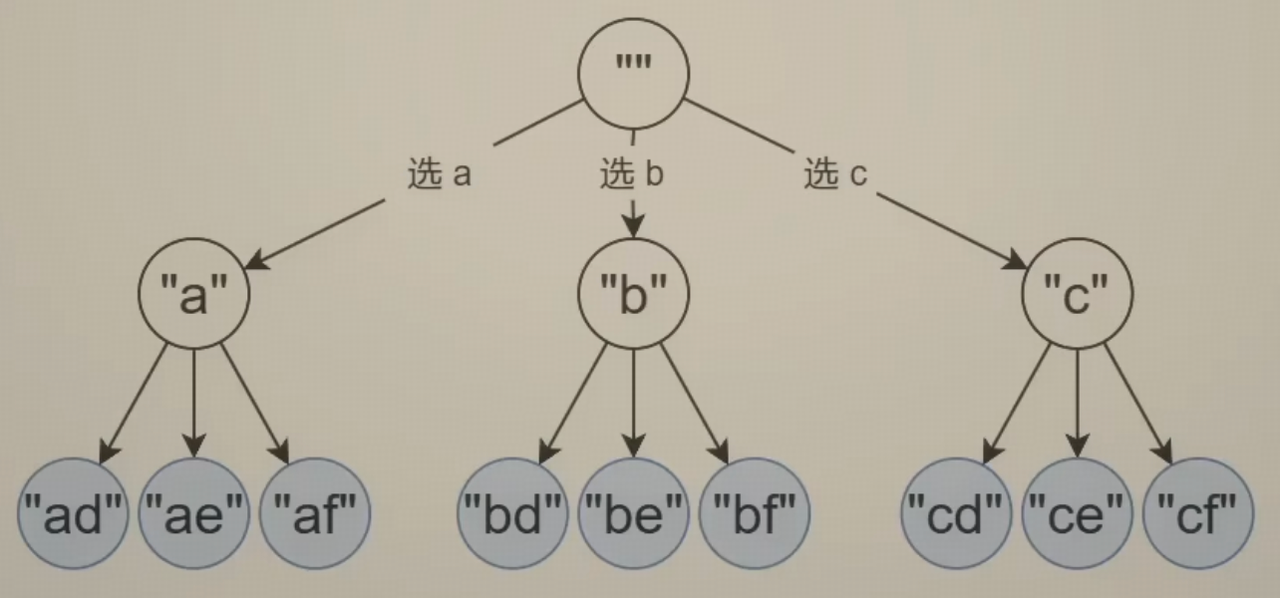
回溯有一个增量构造答案的过程，这个过程通常用递归实现。把这个过程画成一棵树，第一个字母选 a，选 b，选 c，第二个字母选 d，选 e，选 f，以此类推。这个增量构造答案的过程就是回溯的特点。

• “回溯三问”

用一个 path 数组记录路径上的字母

1. 当前操作？枚举 path[i] 要填入的字母

2. 子问题？构造字符串 >= i 的部分

3. 下一个子问题？构造字符串 >= i + 1 的部分

首先需要枚举一个字母，比如字符串的第 i 个字母，同时，为了得到答案，还需要一个全局数组 path 来记录递归路径中枚举的字母。

这里有一个 i，递归的参数也肯定有一个 i。这里需要注意，对于递归参数中的 i，它的含义不是第 i 个，而是下标大于等于 i 的这部分还需要继续枚举，这就自然地引出了子问题。

枚举了一个字母后，下一个子问题是什么？现在已经枚举了第 i 个，那么剩下的就是下标大于等于 i + 1 的这部分了。

这里使用的递归函数名称为 dfs（Depth First Search），是因为这个过程就是在这颗树上做深度优先搜索。

做法

生成的字符串的长度和输入的字符串的长度是一样的。首先需要把数字和要枚举的字母对应起来，用一个 MAPPING 来实现，下标 2 对应着 abc，以此类推。然后获取字符串的长度 n，如果 n = 0，直接返回空数组；初始化答案为空，路径为长度为 n 的数组。接着写递归函数，首先判断边界条件，如果 i == n，说明找到答案了，将数组转换成字符串加入答案中；对于非边界条件，需要枚举第 i 个字母是什么，将它填到 path 中，然后再递归。最后递归入口，返回答案。

MAPPING = ['', '', 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        n = len(digits)
        if n == 0:
            return []
        ans = []
        path = [''] * n

        def dfs(i):
            if i == n:
                ans.append(''.join(path))
                return
            for c in MAPPING[int(digits[i])]:
                path[i] = c
                dfs(i + 1)
        dfs(0)
        return ans

时间复杂度：对于回溯问题，可以从循环的角度来理解，枚举第一个字母就是最外面的循环，第二个字母就是第二层循环，以此类推。最多需要循环 4^n 次，最后生成答案时，需要花费 O(n) 的时间，所以时间复杂度是 O(n*4^n)。

空间复杂度：O(n)。

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

思路1

要想生成所有子集，有两种思路，区别在于当前操作是什么。如果站在输入的角度思考，那就是枚举第i个数，选它还是不选它；子问题就是从下标大于等于i的数字中构造子集；下一个子问题就是从下标大于等于i+1的数字中构造子集。

做法1

首先写非边界条件，如果不选当前数，那么这个数被跳过，直接递归到i+1；如果选当前数，先把这个数加到路径中，然后递归到i+1。由于是在路径后面添加元素，所以递归之前和递归之后需要保持一致，因此在返回之前，需要把路径恢复到递归之前的样子。

写边界条件，把路径中记录的答案加到ans中，由于这个路径是一个全局变量，它是会变化的，所以此时需要把它的答案固定下来，即copy()。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        ans = []
        path = []

        def dfs(i: int) -> None:
            if i == n:  # 子集构造完毕
                ans.append(path.copy())  # 复制 path，也可以写 path[:]
                return
                
            # 不选 nums[i]
            dfs(i + 1)
            
            # 选 nums[i]
            path.append(nums[i])
            dfs(i + 1)
            path.pop()  # 恢复现场

        dfs(0)
        return ans

时间复杂度：每次递归只有不选和选两种情况，所以一共会递归O(2^n)次，再加上copy()的时间是O(n)的，所以时间复杂度就是O(n*2^n)。

空间复杂度：O(n)。

思路2

站在答案的视角，每次必须选一个数，枚举答案的第一个数选谁，第二个数选谁，当前操作就是枚举一个数字，同时注意{1, 2}和{2, 1}是重复的子集，也就是不考虑顺序，那么就规定一个顺序，比如严格递增，那么枚举的数字必须大于上一个枚举的数字，当前操作就是从大于等于下标i的下标j数字中选一个数；子问题是从下标大于等于i的数字中构造子集；下一个子问题是从下标大于等于j+1的数字中构造子集。由于子集的长度没有约束，所以每个长度都可以是答案，那么每次递归都需要记录一下答案。

做法2

将添加答案的代码修改为每次循环都会执行，看做递归到的每个节点都是答案。然后枚举当前要填的数字，把数字加到路径中，递归，恢复现场。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        ans = []
        path = []

        def dfs(i: int) -> None:
            ans.append(path.copy())  # 复制 path
            for j in range(i, n):  # 枚举选择的数字
                path.append(nums[j])
                dfs(j + 1)
                path.pop()  # 恢复现场

        dfs(0)
        return ans

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些 子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。
示例 1：
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

思路1

假设每两个字符之间都有一个逗号，可以对每个逗号考虑是选它还是不选它，这样就转换成了子集问题。

做法1

从答案的视角来分析，枚举第一个逗号的位置，第二个逗号的位置。

当前操作：选择回文子串s[i..j]，加入path；

子问题：从下标大于等于i的后缀中构造回文分割；

下一个子问题：从下标大于等于j+1的后缀中构造回文分割；

这里枚举的逗号位置相当于枚举回文子串结束的位置。

如何判断一个字符串是否回文：1. 相向双指针，分别指向字符串的开始和结束位置，如果相同就各往中间走一步，直到找到不同的，或者左指针大于等于右指针为止。2. 直接把这个字符串反过来，然后和原串比较是否相同。

注意，不是每次递归都添加答案，因为每个字母都需要在答案中，所以必须等到分割结束再加到答案中。

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        n = len(s)
        ans = []
        path = []

        # 考虑 s[i:] 怎么分割
        def dfs(i: int) -> None:
            if i == n:  # s 分割完毕
                ans.append(path.copy())  # 复制 path
                return
            for j in range(i, n):  # 枚举子串的结束位置
                t = s[i: j + 1]  # 分割出子串 t
                if t == t[::-1]:  # 判断 t 是不是回文串
                    path.append(t)
                    # 考虑剩余的 s[j+1:] 怎么分割
                    dfs(j + 1)
                    path.pop()  # 恢复现场

        dfs(0)
        return ans

时间复杂度：O(n*2^n)。

空间复杂度：O(n)。

思路2

输入的视角，逗号选或不选。

假设每对相邻字符之间有个逗号，那么就看每个逗号是选还是不选。

也可以理解成：是否要在 i 和 i+1 处分割，把 s[i] 作为当前子串的最后一个字符，把 s[i+1] 作为下一个子串的第一个字符。

注意 s[n−1] 一定是最后一个字符，所以在 i=n−1 的时候一定要分割。

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        n = len(s)
        ans = []
        path = []

        # 考虑 i 后面的逗号怎么选
        # start 表示当前这段回文子串的开始位置
        def dfs(i: int, start: int) -> None:
            if i == n:  # s 分割完毕
                ans.append(path.copy())  # 复制 path
                return

            # 不分割，不选 i 和 i+1 之间的逗号
            if i < n - 1:  # i=n-1 时只能分割
                # 考虑 i+1 后面的逗号怎么选
                dfs(i + 1, start)

            # 分割，选 i 和 i+1 之间的逗号（把 s[i] 作为子串的最后一个字符）
            t = s[start: i + 1]
            if t == t[::-1]:  # 判断是否回文
                path.append(t)
                # 考虑 i+1 后面的逗号怎么选
                # start=i+1 表示下一个子串从 i+1 开始
                dfs(i + 1, i + 1)
                path.pop()  # 恢复现场

        dfs(0, 0)
        return ans