灵神基础算法精讲-02-学习笔记

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

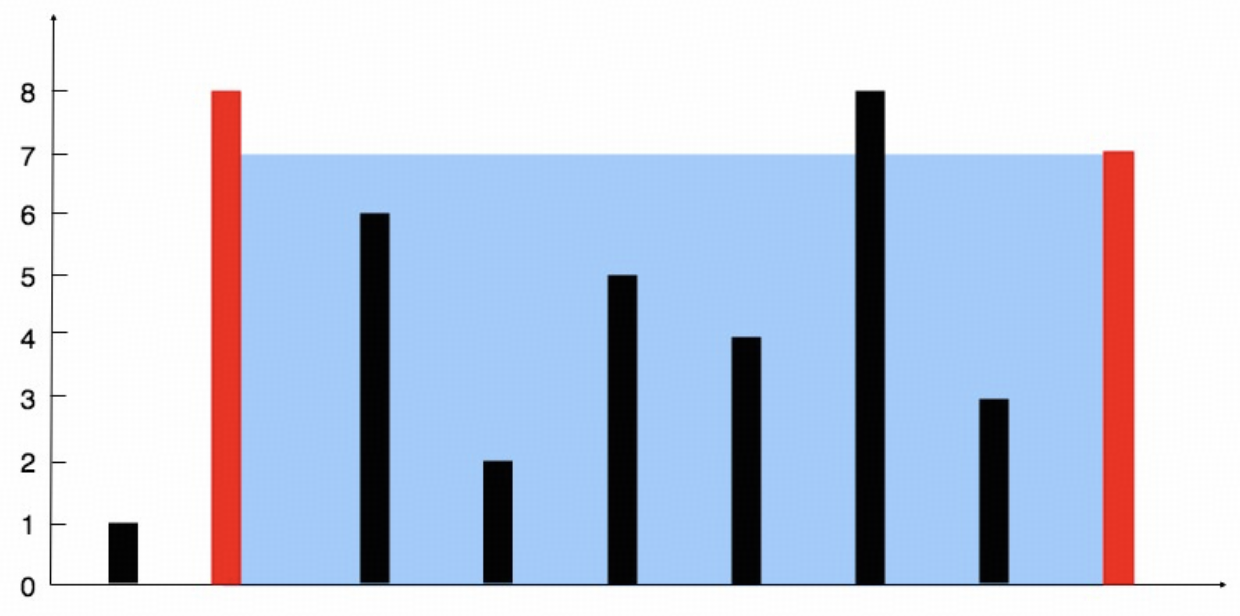
思路

容器的高度取决于容器两端更短的那条边，容器的宽度取决于容器两端之间的距离，也就是下标的差。

思考短的那条边，如果它和中间的边构成容器，可以分类讨论：

1. 如果中间的边比它短，那么容纳的水宽度减少，高度也减少，那么肯定不会比当前容纳的水多。
2. 如果中间的边比它长或者一样长，那么容纳短水宽度减少，高度不变，也不会容纳更多的水。
   因此，中间的任何边都无法和它构成一个容量更大的容器了。

换句话说，如果要找到一个容量比当前区域更大的容器，那么肯定不会包含当前这条更短的边，所以可以直接去掉，在剩下的边中继续寻找。

做法

初始化两个指针，L = 0，R = n - 1，n是边的个数，两个指针分别指向最左和最右的边，哪条边短就移动哪条，如果一样长，移动哪个都可以。在移动之前，先把这两条边围成的面积计算出来，如果比答案大就更新答案。

class Solution:
    def maxArea(self, height):
        ans = 0
        left = 0
        right = len(height) - 1
        
        while left < right:
            area = min(height[left], height[right]) * (right - left)
            ans = max(ans, area)
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1
        return ans

时间复杂度：每次花费O(1)的时间就去掉了一条边，所有指针加起来移动的距离是O(n)，所以时间复杂度是O(n)。

空间复杂度：只用到了几个额外变量，所以空间复杂度是O(1)。

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

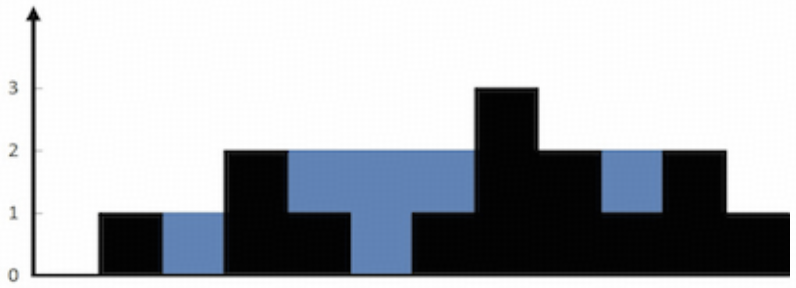
思路

假设每个位置有一个宽度为1的桶，要计算每个桶能接多少水，就需要计算左边这块木板的高度和右边这块木板的高度，这两个取最小值，左边木板的高度取决于左边的最大高度，右边同理。

做法1

需要用到两个额外的数组，第一个数组存储从最左边到第i个位置的最大高度，即前缀的最大值；第二个数组存储从最右边到第i个位置的最大高度，即后缀的最大值。对于每个前缀最大值，可以用上一个前缀最大值和当前高度，这两个取最大值就能够得到当前的前缀最大值。后缀最大值从右到左算。最后同时遍历前缀最大值、后缀最大值和当前高度，取前缀最大值和后缀最大值中小的那一个减去当前高度就是当前下标能够接到的水，把每个水桶能接到的水都加起来就是答案。

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        pre_max = [height[0]] + [0] * (n - 1)
        suf_max = [0] * (n - 1) + [height[-1]]
        ans = 0

        for i in range(1, n):
            pre_max[i] = max(pre_max[i - 1], height[i])

        for i in range(n - 2, -1, -1):
            suf_max[i] = max(suf_max[i + 1], height[i])

        for p, s, h in zip(pre_max, suf_max, height):
            ans += min(p, s) - h
        
        return ans

时间复杂度：在计算前缀最大值、后缀最大值以及计算答案的过程当中都是一次遍历，这样就用O(n)的时间解决了问题。

空间复杂度：创建了两个大小为n的数组，所以空间复杂度为O(n)。

做法2（空间优化）

假设已经算出了一部分前缀的最大值和一部分后缀的最大值，如果前缀最大值比后缀最大值小，那么左边这个木桶的容量就是前缀最大值减去当前木桶高度，否则就计算右边。

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
        ans = 0
        left = 0
        right = n - 1
        pre_max = 0
        suf_max = 0
        # 不用加等号，因为相遇的位置一定是最高的柱子，这个柱子是无法接水的
        while left < right:
            pre_max = max(pre_max, height[left])
            suf_max = max(suf_max, height[right])
            if pre_max < suf_max:
                ans += pre_max - height[left]
                left += 1
            else:
                ans += suf_max - height[right]
                right -= 1
        return ans

时间复杂度：一次遍历，每次操作只花费O(1)的时间，O(n)的时间解决了问题。

空间复杂度：只用到了几个额外变量，所以空间复杂度为O(1)