灵神基础算法精讲-01-学习笔记

167. 两树之和 Ⅱ - 输入有序数组

给你一个下标从1开始的整数数组numbers，该数组已按非递减顺序排列，请你从数组中找出满足相加之和等于目标数target的两个数。如果设这两个数分别是numbers[index1]和numbers[index2]，则1 <= index1 < index2 <=numbers.length。

暴力做法

枚举第一个数（一个for循环），然后在后面枚举第二个数（一个for循环）。for循环嵌套for循环，时间复杂度为O(n^2)。

暴力做法没有利用到数组已经排序这个性质。

思路

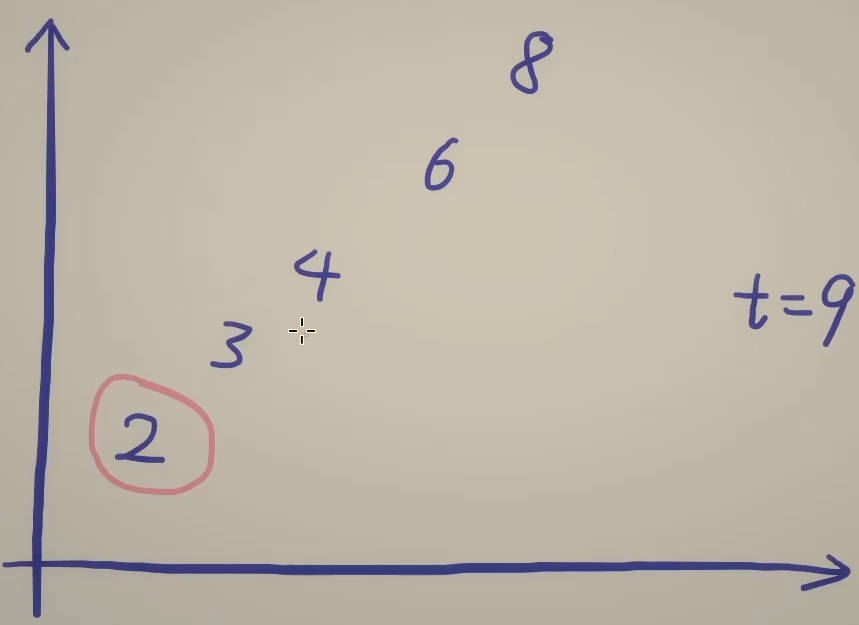
首先选最小的数和最大的数相加，若相加大于target，则他俩之间的所有数和最大的数相加肯定也大于target，直接把最大的数去掉，从剩下的数中寻找答案；若相加小于target，则他俩之间的所有数和最小的数相加肯定也小于target，直接把最小的数去掉，从剩下的数中寻找答案，以此类推。

暴力做法是找两个数加起来和target进行比较，花费O(1)的时间就只知道了O(1)的信息。

优化后的做法是把当前剩下的最小的数和最大的数加起来和target进行比较，比完之后就知道其中一个数和其它任何一个数相加都是小于或大于target的，花费O(1)的时间知道O(n)的信息。

优化的前提是数组是排好序的，如果数组是没有排好序的，那么就不能使用这个算法。

做法

初始化两个指针left和right，分别是0和n-1，如果这两个指针指向的数字之和恰好等于target，则返回这两个下标；如果大于target，就去掉最大的数，把右指针向左移动；如果小于target，就去掉最小的数，把左指针向右移动。

# 输入：numbers = [2, 7, 11, 15], target = 9
# 输出：[1, 2]

class Solution:
    def twoSum(self, numbers, target):
        left = 0
        right = len(numbers) - 1
        while True:
            sum = numbers[left] + numbers[right]
            if sum == target:
                break
            if sum < target:
                left += 1
            if sum > target:
                right -= 1
        return [left+1, right+1]

    
if __name__ == "__main__":
    numbers = [2, 7, 11, 15]
    target = 9
    solution =  Solution()
    print(solution.twoSum(numbers, target))

15. 三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

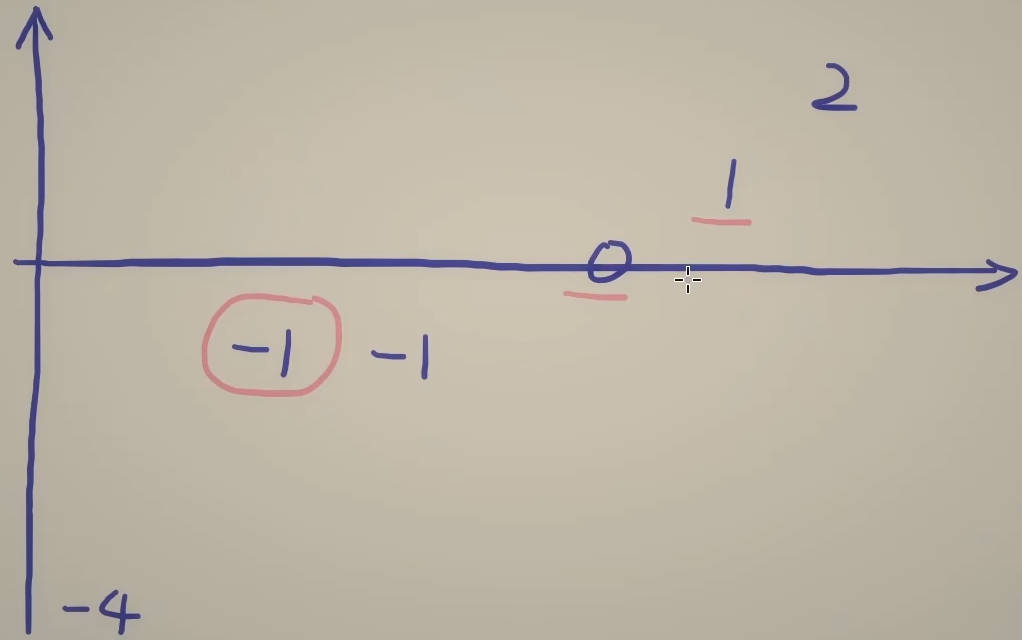
思路

先排序，然后利用相向双指针，问题转换成剩下的两个数相加等于-nums[i]，如果当前枚举的这个数和上一个数是相同的，直接跳过这个数。

做法

枚举第一个数i，从0枚举到n-3，留两个余量。

如果第一个数的下标大于0且该数等于上一个数就continue，因为不能有重复的三元组。

初始化第二个数和第三个数j、k，接while循环，条件为j < k。

while循环内首先求三数之和，如果大于0，k -= 1；如果小于0，j += 1，否则找到答案，ans.append存储答案，还要在这里将重复的j和k也跳过: j += 1, nums[j] == nums[j-1], continue; k -= 1, nums[k] == nums[k+1], continue。

优化

如果当前i对应的x和其它最小的两个数之和都大于0，则break，后续没有机会等于0。

如果当前i对应的x和其它最大的两个数之和都小于0，则continue，后续还有机会等于0。

class Solution:
    def threeSum(self, nums):
        nums.sort()
        n = len(nums)
        ans = []
        
        for i in range(n-2):
            x = nums[i]

            if i > 0 and x == nums[i-1]:
                continue

            if x + nums[i+1] + nums[i+2] > 0:
                break

            if x + nums[n-2] + nums[n-1] < 0:
                continue


            j = i + 1
            k = n - 1
            while j < k:
                sum = x + nums[j] + nums[k]

                if sum < 0:
                    j += 1
                if sum > 0:
                    k -= 1
                else:
                    ans.append([x, nums[j], nums[k]])

                    j += 1
                    while j < k and nums[j] == nums[j-1]:
                        continue
                    
                    k -= 1
                    while j < k and nums[k] == nums[k+1]:
                        continue

        return ans
    
if __name__ == '__main__':
    
    solution = Solution()
    nums = [-1, 0, 1, 2, -1, -4]
    print(solution.threeSum(nums))